Month: February 2007

Blast From the Past: Talking Head

I’m on a mailing list for my old school, and the topic came up of if there are any good online text-to-speech tools. Someone posted this link. Wow, I thought. I immediately recognized the application.

Back in 2001 I worked for a little internet startup called Oddcast Entertainment. I was one of the main developers for an online character application, a prototype that we were fashioning into a product, complete with end-user authoring tools. One of the first things I did was integrate a text-to-speech engine into the system, and as a proof-of-concept I made a demo, which, although re-skinned, is essentially what you see here. I always thought it was a cool little thing that shows off the technology, and is fun and interactive in the sense that you get to hear it say what you type. My original version had a much larger text entry box, and I used to test it on the poetry of Robert Frost and Lewis Carroll. On the way to being productized, the text to speech part was buried in a much larger feature set, and I did not know they kept around a link to this app. So I’m happy to have found this page.

Origami Polyhedra: The Stellated Dodecahedron Part 2

A little while ago I posted some pictures of Stellated Dodecahedra I made in origami. Here the crease patterns for them. You see, in addition to folding origami, I’ve taken an interest in diagramming, and someday I hope to publish a book of my models. But I find diagramming so laborious that I only do one model a year! (Although they do tend to be pretty complex models.) I’ve also been developing crease patterns, which is particularly useful for polyhedra and other complex subjects where there is a lot of prefolding.

I do my diagramming and CP’s in Flash, and I’m not aware of other people doing this. One reason is I use Flash a lot in my day job, so I know it and can work in it quickly. Another is that I can use to make animated diagrams and CP’s. You can see some of them on my main origami page. This is an experimental format which I am refining over time. It had its origin in the Foldinator Project. Foldinator was originally envisioned as a full-on authoring tool for modeling origami and creating printable diagrams. However, to get there is a rather major development effort. So instead I wound up with this little hacker-level tool that I use. I still hope to finish and release Foldinator someday, but I’d need to treat it like a professional software development project and devote something like 6 months to a year of full-time work to it. Ah well, maybe if I’m lucky I can do like Robert Lang and retire young to do origami full-time.

Meanwhile, you can see the various approaches for the Stellated Dodecahedron.

Here is the one made from two squares. As you can see it’s the simplest of the bunch.

Next up is the one folded from a 2:1 rectangle. This one is remarkably efficient in it’s use of paper, to the point where I had to set it into a larger area to have paper to do the joining. It’s also kind of cool because it has a sort of zigzag layout. I plan to publish an animated CP of this one shortly.

Lastly is the “classic” version, from a single square. This is foldable but very difficult. I like the CP a lot because of the way the layout maximizes the root pentagon and underlying square. Vertices of the finishes form touch 3 edges of the paper. This one would be a good for an animated CP as well.

Happy Valentine’s Day

Although Valentine’s Day was in the middle of last week, today was the much-coveted day off from work, which are rare nowadays since I just started a new job. Thank you George and Abe! I got caught up on my rest and had some good quality time with my kids and their legos. My daughter Lizzy (age 7) and I came up with this:

Happy Valentine’s day everyone! The squares represent chocolates, or candies of any conceivable variety. Lizzy also came up with this:

A house and yard with a swimming pool for her favorite Littlest Pet Shop pet, Chippy the Hamster. This kind of mirrors her online world these days. She’s really into WebKinz and just got a yard and swimming pool for her pet Buttercup, an alley cat.

Extreme Yes for Strings

If you’re anything like me, and I know I am, you’ll fondly remember Yes as one of the all-time great prog rock bands, known for their sweet harmonies and expansive, even epic compositions. Their radio-friendly sound served as a gateway prog band to turn kids on to other, weirder, edgier groups like King Crimson, and, well pretty much anything Bill Bruford has ever done.

Back in the 80’s I was in a prog rock band, Infinigon, that did our share of Yes covers. The bass player in the group was the inimitable John J. Neumann, who is also a recording artist and accomplished classical violin player. He recently completed an adaptation of Yes’s Tales From Topographic Oceans for string quartet. Unlike the original, which is a bit long and rambling, John’s version features only best parts. You can check it out here, along with a bunch of his other musical projects.

Enjoy!

Origami Polyhedra: The Stellated Dodecahedron

As long as I can remember I’ve liked geometry.

I’ve been doing origami polyhedra for quite some time, and you can see some of the ones I’ve designed on my Origami Page. My approach is mainly from single sheet, in contrast the more common modular approach. When I first started, I thought that it was new, largely unexplored territory, and I could do something really interesting. Soon I could see it was a rich area of endeavor, but also very challenging. Around that time I met John Montroll, and he was way ahead of me down this path. In fact he was about to release a book on origami polyhedra, and was working on a second one. This was great for me, because he was eager to have people test his diagrams, and was very generous with his ideas, and I learned a lot from our discussions. On the other hand, he pretty much had the basics covered and then some, like several versions of the platonic solids, and some prisms and Archimedean solids and other shapes. So I had to go a good deal further to get into original territory.

One of my all-time favorite shapes has always been the Stellated Dodecahedron, which is the 3-D analog of the pentagram. (Which, BTW is the 4D analog of the Tetrahedron, but since no one folds 4-D origami, that’s a bit outside the scope of this discussion.) I’ve designed and attempted to fold various versions of this shape over time.

Here is a design from a single square. I actually succeeded in folding one, from a giant (24″) sheet of foil paper. It worked, but I would not call the result great in terms of the level of craft. I tried another from a smaller (14″ or so) piece of thickish (for origami) paper, but never completed it. The problem is that once you get towards the end, there are many flaps of extra paper to deal with, and the model wants to spring apart. This, combined with the limitation of having only two hands, makes it very tricky to close. I may give this design another try, but I’ve been exploring other avenues.

Last summer at the OUSA Annual Convention I was playing around with ideas for this shape again, and it occurred to me to try it from a 2:1 rectangle. It was still a single sheet, but provide more edge relative to the paper’s area, so it ought to reduce the problem of extra flaps of paper to hide. I have a design for a 2:1 icosahedron which is really efficient and easy to fold, and it didn’t take too long to come up with a regular dodecahedron, which is the base for the stellated version. When I went ahead and folded it, it realized it was so efficient that there was not enough paper to make a lock, so I’d need to go back and modify my design be setting it into a slightly larger rectangle. So I tried again. Still making the model close was a bit of a challenge. Doable, but requiring some effort.

Then over Christmas vacation, I finally had some origami time again, and this time I went for a version made from 2 squares, each of which comprise half the finished model. This is much easier to fold because you can reach inside each half as you’re making it, and the leftover flaps of paper become tabs that fit into the opposite half, nicely solving the problem of what to do with the leftover bits. At the end, the two halves lock together tightly and securely. The resulting model is quite attractive, because it’s much easier not to crush it as you’re putting it together. The examples below are made from (2 sheets each of) 6″ foil paper and 8.5″ photocopy paper.

Which brings up the question: Origami purists like to only work for a single square sheet. Which is more of a “cheat”: to use two squares or one rectangle?

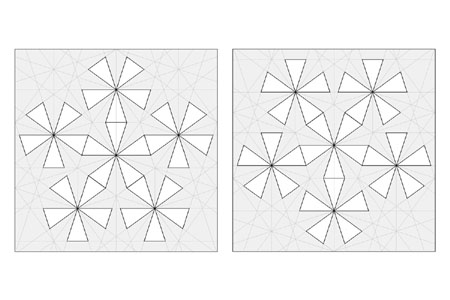
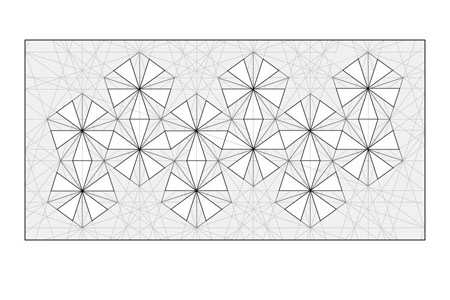
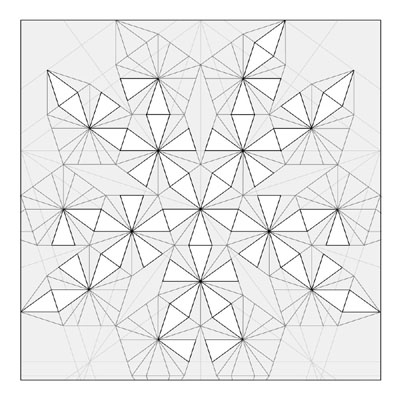
Coming Soon: crease patterns for the 3 methods for Stellated Dodecahedra.

Mostly Styley

Well, I managed to get the header looking like I wanted to, but it was kind of tricky. Unlike the rest of the style stuff, which is under the control of css and various other config files, the header is under the control of some WYSIWYG tool, that has limited flexibility. If you drill down under that, looking the files on the server directly, you’ll find its a combination of an image file and a php script. So I replaced the file with one that looked like I wanted, and commented out the script, but that just made the tool auto-generate it’s idea of default header. You I had to un-bypass that and edit the script to render the header to match the header image I made. Whew, weird. It’d be better if they had an option upload a header image. Next time I get into the appearance of the blog, it’ll be to make a (fancier) custom header image. Still the site looks good for now.

Semi Styley

Well, I got about halfway thru putting together a new style. The main thing now is to get a new header graphic. Unfortunately, I haven’t been able to anything in the various style and config files available that lets me affect the header in any way! Ah well I guess that’ll have to wait for another night; it’s getting late.